相关性如何运作
当变量相关时,一个变量可以用来估计另一个变量。相关性在数据分析和预测中非常有用。
在真实世界的数据集中,我们经常发现两个指标或变量非常相似。我们称这些变量为“相关”。了解两个指标是相关的很有用,因为它允许我们根据一个值来估计另一个值。
例如,如果我们发现我们的冰淇淋店在晴天卖出更多的冰淇淋,这将使我们能够根据天气预报来推测我们的销量。真正的原因可能不是阳光(也许是温度?),但强大的相关性仍然意味着我们的估计会比不猜测时更准确。
一个常见的误解是认为两个变量之间的相关性意味着存在因果关系。但相关性仅仅是统计关系的观察。夏季冰淇淋销量增加的真正原因可能是游客数量,而游客倾向于在夏季出行。阳光仍然是估计冰淇淋销量的有用代理,但它不是根本原因。
什么是相关性?
相关性定义为两个变量或指标之间的相互关系。直接相关(也称为正相关)意味着一个变量的值越大,另一个变量的值也越大。反向或负相关意味着当一个变量的值越大时,另一个变量的值就越小。
直接和反向相关性可以具有不同的强度。数字的关联性越紧密,相关性就越强,无论关系是直接还是反向的。
当没有相关性时,变量之间没有可识别的联系。也许我们卖的是卫生纸而不是冰淇淋。我们的销量每天都会略有变化,但阳光增多似乎并不能帮助我们卖出更多,阳光也不会减少我们的销量。
如何衡量相关性
我们通常用一个数字来衡量相关性,称为 皮尔逊相关系数,皮尔逊 r,或简称 r。它的值在 –1 到 +1 之间,指示了相关性的方向和强度。
- r = +1:完美的正向关系(一个指标的值越高,另一个指标的值也越高)
- r 在 0 和 1 之间:正相关,越接近 1,相关性越强
- r = 0:无关系
- r 在 0 和 -1 之间:负相关,越接近 -1,相关性越强
- r = –1:完美的负向关系(一个指标的值越高,另一个指标的值就越低)
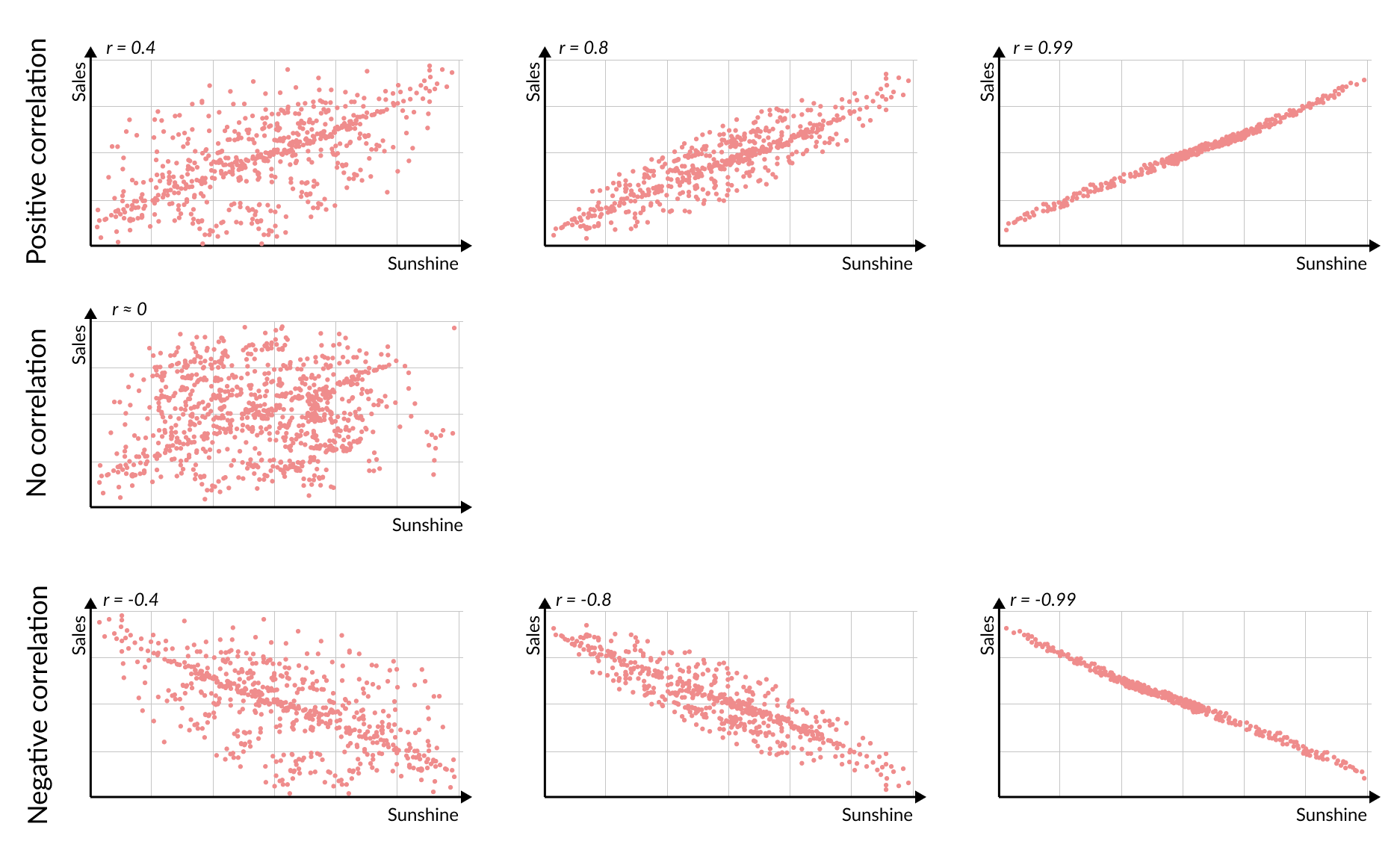
在我们的冰淇淋销售例子中,强的正相关(例如,r = +0.8)意味着温暖的日子通常伴随着更高的销量。r 约等于 0 表示没有明显的模式,而负 r 表明炎热的日子与销量下降同时发生。
我们可以通过散点图直观地看到相关性:形成清晰上升直线的点表示强的正相关(高 r),而分散的点表示较弱或无相关性。
解释力
当两个变量 A 和 B 相关时,我们可以简单地假设 B 的值就是 A 的值。如果我们知道 A,我们也知道 B。当然,这种完美相关(r = 1)在实践中几乎是不可能的。但是 B 的值有多少是由 A 决定的(反之亦然)?
下图可视化了这种预测关系。直线代表了期望值,而单个点显示了实际数据点偏离该估计值的情况。
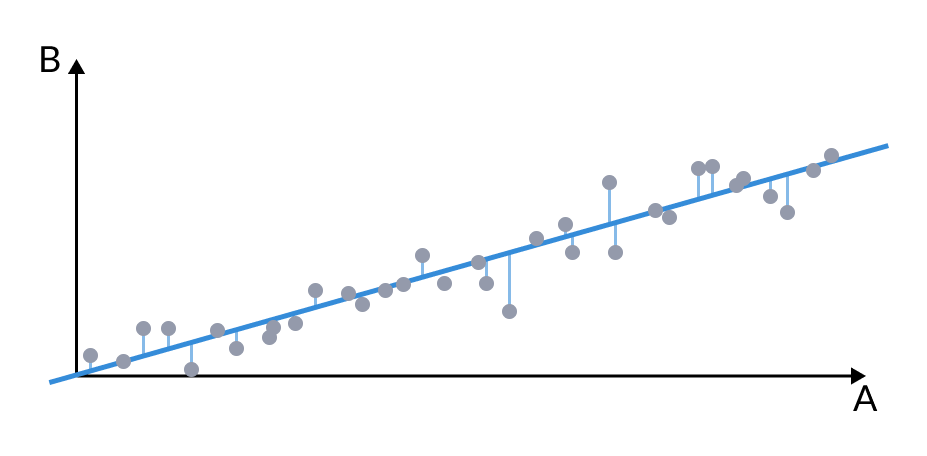
为了量化 B 中有多少可以被 A 预测(反之亦然),我们使用 r-squared (r²)。通过将相关系数 r 平方,然后乘以 100,我们得到一个百分比,揭示了输入变量在多大程度上可以解释目标变量的方差。
如果阳光和冰淇淋销量之间的相关性是 0.7,那么 r² 是 0.49(或 49%)。我们可以解释约 49% 的销量波动是由温度引起的,其余 51% 是由其他因素(如节假日或设备故障)造成的。
辛普森悖论:数据的子集可能存在反向相关
到目前为止,我们都是一次性考虑整个数据集。但是,当我们把数据分解成子集并在每个子集上计算相关性时,我们经常会发现整体相关性的令人惊讶的逆转。
例如,考虑学习时间和学生考试成绩之间的关系。在每所学校,我们可能会发现学习时间和考试成绩之间存在正相关,但如果我们观察三所不同学校的所有学生,趋势可能会出现逆转。这种逆转可能归因于更具挑战性的学校需要花费更多的时间学习,但仍然导致较低的成绩。
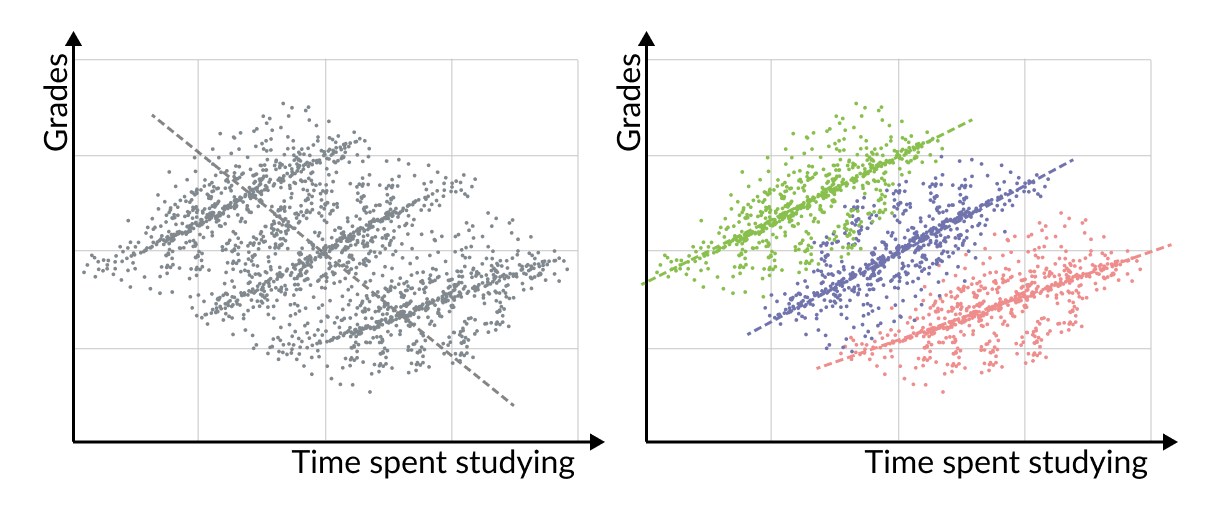
子集的相关性与整个数据集相反的情况通常被称为 辛普森悖论,这是一个不幸的名字,因为它是一个相当普遍现象。
当我们查看整个数据集时,它可能显示一个整体的相关性(例如,负相关),但在我们将数据集分成子组时,其中一些子组通常会显示相反的相关性(例如,正相关)。甚至所有子组都显示相反的关系也并不罕见。
辛普森悖论的核心是,整体相关性以及子集内的相关性都是真实且正确的。在我们学生的例子中,当考虑所有学生时,更多的学习时间会导致更低的成绩,并且当我们查看每个单独的学校时,花费更多时间学习意味着更好的成绩,这都是真实的。
对于实际的数据分析,数据子集内的相关性通常更重要,因为它们避免了不同类型因素的组合(例如我们例子中的不同学校)。
相关不等于因果
仅仅因为两件事一起变动,并不意味着其中一件导致了另一件。这是一个常见的陷阱,因为相关性常常被这样呈现(包括在我们上面的冰淇淋销售例子中)。当我们说“A 和 B 相关”时,可能暗示 A 导致 B 的值按其方式变化。然而,这并非相关性的含义。冰淇淋销量与阳光的相关性为 0.7 与阳光与冰淇淋销量的相关性为 0.7 是相同的陈述。
虽然强的相关性通常表明存在潜在的联系,但它可能是间接的,或者涉及到隐藏的变量。相关性是提出问题的良好起点,但它不是最终答案。

